Armageddon Chess - a bidders guide
One of the problems for chess contests is forcing a result. There are three possible outcomes for any given game (white wins, a draw, white loses) and any contest could continue indefinitely as both sides draw repeatedly. One solution to this problem is armageddon chess. This version of chess is played where black gets “draw-odds” (black wins if it’s a draw). This is a big advantage, so to compensate for this advantage, white usually gets additional time. Some tournaments set this time in advance (a common one is white has 5 minutes, black has 4 minutes without increment) but it’s becoming increasingly common to have a bidding system. Before the game, both players “bid” a time they would be willing to play black with. The lower time then has to play with black against whatever fixed time is set for white. For example, at the Airthings Masters (see tweet) both Carlsen and Nakamura bid very similar times for black, but Carlsen was 1 second lower, so he took the black pieces.
A question one might want to answer is: “What is the optimal strategy for bidding?”. Before we think about this question, we should try and answer the (simpler) question “what is the fair rate for black?”.
In order to start answering that question, we need to understand a little bit about the rate of draws in chess.
How rating affects the rate of draws (in classical chess)
One stylised fact that most chess players know is that the higher rated players are, the more frequently they draw. In order to gauge how much of an effect this was, I plotted average Elo vs draw rate across a range of different Elos for classical chess.
Note two interesting things:
The draw rate does indeed increase with the strength of the players
The draw rate is heavily influenced by who has black.
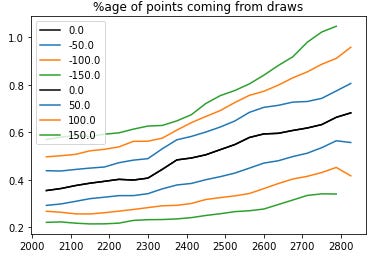
If the stronger player has black, the draw rate is much higher than when white is stronger. This isn’t quite as asymmetric as this plot makes it appear. In terms of “proportion of points” coming from draws vs wins, the pattern is fairly symmetric:
The way to read this is “when white is underrated by ~150 points, at all levels white scores more than 50% of their total score by drawing”. “when white is overrated by ~150 points, at all levels white scores >70% of their score from winning”. (Score here is 1 for a win 1/2 for a draw and 0 for a loss). (Note also that at the highest levels, they are scoring more in draws than Elo says they should score at all - this isn’t completely shocking, we know Elo struggles for large rating games).
How rating affects the rate of draws (rapid and blitz)
Producing the same charts as above for blitz chess. (Specifically 5 minute chess, of which the vast majority of games in my dataset are 3+2 (3 minutes for the game with a 2 second increment each time a player makes a move)). One thing to note is the draw rate is much lower than in the classical games. Another thing to consider is how much less linear the draw rate is with Elo.
How does chess performance change with time-control
In order to appreciate what black is giving up by having less time on their clock, we need to understand how performance varies with time-control.
Ken Regan briefly discussed how much time affects intrinsic performance in chess on the Perpetual Chess Podcast. Specifically the slower the time control, the stronger players perform. Using his main model, a player in our 5 minute chess should be operating at an Elo roughly 565 points lower than they are in the classical chess we were looking at in our earlier model. It’s not necessarily the case that players are playing the same at faster time controls as the equivalent lower rated players. (In particular, we might expect the blunder rate to be worse than a typical player of that level but the positional understanding and openings to be better). A question we might want to answer is: “is performance degregation alone enough to explain the higher draw rates of faster chess?”
Is the lower draw rate explained by ‘worse’ chess being played?
No.
Fitting the draw rate at various different time controls for Elos 2000+ followed by shifting according to the Regan model, we easily see that there is a large divergence between different time controls and draw rates (for equally rated players):
How should one bid in armageddon chess?
Now we know what the draw rate is for any given time control and playing strength, we should be able to figure out the “fair” bid for a given player. The “fair” bid is the time where the player has equal chances of winning with black as with white.
Let’s start with the example of Carlsen (2852) v Nakamura (2768), with 15 minutes, no increment as our time control.
Assuming both players had 15 minutes, we would expect a w/d/l as follows:
So Carlsen with black and draw-odds is ~84% to win, and Carlsen with white (and without draw-odds) is ~42% to win. Thefore we should expect Carlsen to be comfortable giving up some time (and Elo) in order to increase his chances of winning. Essentially our model consists of
Reduce our time
Reduce our Elo according to Ken Regan’s model for the time given up
Adjust the draw rate for the new ratings
Calculate the w/d/l for the new ratings
Repeat except reducing our opponents time
Check that win with white is roughly equal to win + draw with black
If Carlsen bid 8:45, then we’d expect his Elo to drop off by ~110 points. (Or Nakamura’s would drop off by the same more more). His chances of winning with white and black would then be:
This equates to a ~65% chance of winning with white OR a 65% chance of winning with black + draw-odds. All of this should be the same from Nakamura’s perspective, so we should expect them both to bid for similar times, around 8:45. This is fairly close to what they actually bid, and I imagine they have both more data and a better understanding of each other. It’s interesting to me that the theory lines up so neatly with the practice here.
Coda: Norway Chess Armageddon
At Norway Chess, there have been Armageddon tie-breaks after each game for the past few years. The format is 10m for white, 7m for black. In my dataset the average player rating is 2766. Our model would predict for (equally rated) players white to win ~53% of the time in for this format. In reality, white has won 34 / 64 = 53%. Spot on - although probably luck rather than judgement. What would be fair? My model says ~7:35. (Although if I were advising Norway chess, I’d advocating the bidding model - avoids any unfairness resulting from model error and leaves it up to the players to figure out what’s fair).